51_N-Queens

[Hard][Backtracking]

The n-queens puzzle is the problem of placing n _queens on an _n×_n _chessboard such that no two queens attack each other.

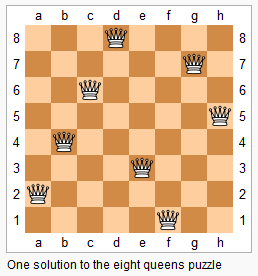
Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where'Q'and'.'both indicate a queen and an empty space respectively.

Example:

Input:
 4

Output:
 [
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.

Solution: Backtracking

Idea:

• Go through row by row. Start from the top row.

• For each row, check if it's possible to put queen in each column.

• If assigning queen to current column violates current assignment for rows on top of current row, go to next column.

• If the entire row has nothing works, backtrack to next column on last row.

• If we have finished the last row, append the assignment and backtrack to last row.

Note that to store the position of assigned queens, we only use an array of length n letting each element indicate the column for ith row.

Time Complexity: $O(n^n)$ not considering prune. Not sure how many will be pruned. It is conjectured to tend to $\frac{n!}{c^n}$ where $c \approx 2.54$

Space Complexity: $O(n)$

def solveNQueens(n):
    """
    :type n: int
    :rtype: List[List[str]]
    """
    def helper(row):
        if row == n:
            output.append(list(col_index))
            # important to use list here, otherwise all output will be the same
            # because of copy reference
            return
        for col in range(n):
            if all(abs(col-b) not in (0, row-a) 
                   for a, b in enumerate(col_index[ :row])):
                col_index[row] = col
                helper(row + 1)

    output = []
    col_index = [0] * n
    helper(0)
    return [["."*col + "Q" + "."*(n-col-1) for col in sol] for sol in output]