Tower of Hanoi

[Math, Recursion]

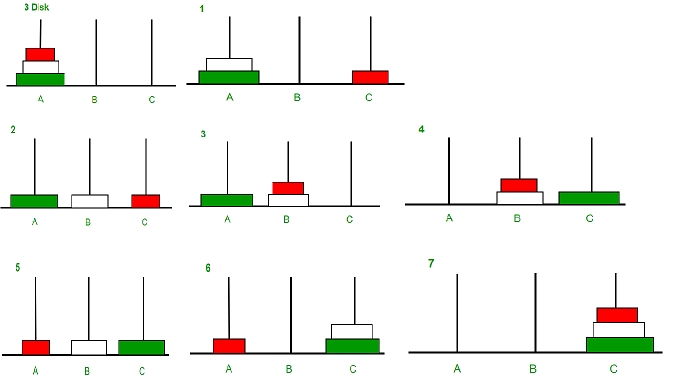
Tower of Hanoi is a mathematical puzzle where we have 3 rods and n disks. The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:

1. Only one disk can be moved at a time.

2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.

3. No disk may be placed on top of a smaller disk.

Write a program which prints a sequence of operations that move n disks from one rod to another.

Example for 3 disks:

Reference: EPI python, page 226

Solution: Recursion

Idea:

• Use recursion. Think about if we know how to move the top n-1 disks, how can we move n disks.

Time complexity: $O(2^n)$ because in the recursion we have $T(n) = 2 T(n-1) + 1$

Space Complexity: $O(1)$

def tower_of_hanoi(n):
    # Recursive function to solve tower of hanoi   
    def helper(n , from_rod, to_rod, aux_rod): 
        # this recursion covers base cases

        # move top n-1 disks to aux_rod
        helper(n-1, from_rod, aux_rod, to_rod) 
        # move the nth disk to to_rod
        print "Move disk",n,"from rod",from_rod,"to rod",to_rod 
        # move top n-1 disks to to_rod
        helper(n-1, aux_rod, to_rod, from_rod) 

    helper(n, 'A', 'B', 'C')  
    # A, C, B are the name of rods